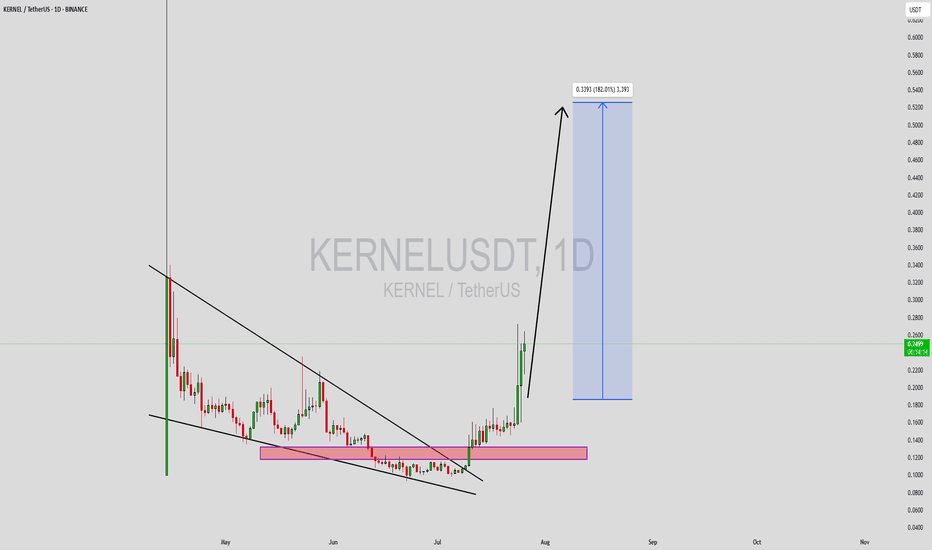
KERNELUSDT Forming Falling WedgeKERNELUSDT has recently completed a significant technical breakout from a well-defined falling wedge pattern, which is known in crypto trading for its strong bullish implications. The asset had been consolidating within this wedge for weeks, forming a base in the demand zone highlighted in the pink region on the chart. Now, after gaining enough strength and momentum, it has broken through resistance with solid bullish candles, signaling the start of a potential parabolic move.
Volume confirmation during the breakout phase is notable—indicating real buying interest rather than a false breakout. Based on this breakout and the current momentum, the expected gain is projected between 170% to 180%+, and the measured move target points toward the $0.33–$0.34 region. KERNELUSDT’s price action has shifted from accumulation to expansion, often the most profitable phase for trend traders. With higher highs and higher lows starting to form, bulls are in clear control.
In addition to the technical pattern, KERNEL appears to be attracting attention from investors, potentially due to its tokenomics, project fundamentals, or upcoming developments. Traders looking for high-reward opportunities with favorable entry points may find this setup ideal, particularly with the recent retest of the breakout zone acting as confirmation. If momentum continues, this rally could easily extend beyond the projected zone.
This is a textbook example of a reversal structure evolving into an explosive breakout. KERNELUSDT is now trending upward strongly, and staying updated on volume surges and any pullbacks to the breakout zone can help traders ride the wave efficiently. The crypto market rewards breakout traders when strong technicals align with market sentiment—and this is one of those moments.
✅ Show your support by hitting the like button and
✅ Leaving a comment below! (What is You opinion about this Coin)
Your feedback and engagement keep me inspired to share more insightful market with you!
Kernel
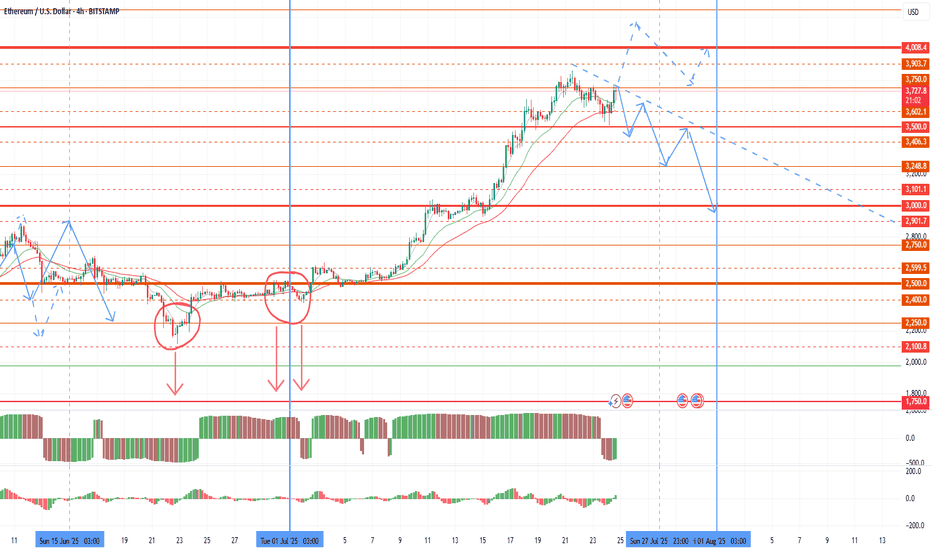
Possible market drawdown before the end of the monthToday I want to review the market and give a warning on further purchases. Since the last review, as expected, volatility in the market began to grow with a flat of about 2500 on ether until the half-year change. The growth of the euro and oil gave rise to a 4k retest in the new half of the year. However, the half-year has opened below 2,500, which is a technical selling signal that bears will use at the end of each major period. A large volume of sales was also left before the half-year change, which can be retested up to 2100-2250. The first pullback is already possible for the current monthly candle, with its pinbar reversal up to 2750-2900 on ether. This pullback started yesterday and is likely to accelerate in the last weekly candle of the month. Further sales are highly likely to continue in the first half of the new month as part of the shadow drawing for the new monthly candle. In an optimistic scenario, the bulls will be able to take 4,000 by the end of the week, in which case the pullback on the current monthly candle will be compensated.
Given the increased likelihood of sales in the market, I recommend fixing profits by the end of the week and reducing the number of coins in operation. The current rollback for some coins will also end with the assignment of the monitoring tag at the beginning of the month and a further collapse, which puts pressure on the coins.
Most of the coins that I considered for work provided good opportunities for making money, especially the growth impulses of pivx and data with sharp breakouts stood out. Adx fio chess cos token also showed growth, but at a smoother pace. The most negative dynamics was given by slf, which eventually received the monitoring tag, and I will not consider it in the future.
Despite the pleasant impulses of 50%+ for individual fantokens, this group as a whole shows extremely negative dynamics relative to the market, and remains in the most oversold position, even relative to coins with the monitoring tag. In an optimistic scenario, fantokens will become interesting to speculators against the background of the general decline of altcoins that has begun, and we can expect a good bull run on them before the end of the month. In a negative scenario, binance may be preparing to assign the monitoring tag to some tokens of this group or chz. In this regard, I leave such tokens as atm acm city porto Lazio as the most undervalued in a small lot. But at the beginning of the month, I also recommend keeping short stops on them in the first half of the day of the first week of the new month to insure against assigning the monitoring tag. Or temporarily sell them for a given period.
In addition to fan tokens, I will choose new coins for operation after assigning the monitoring tag in the new month.
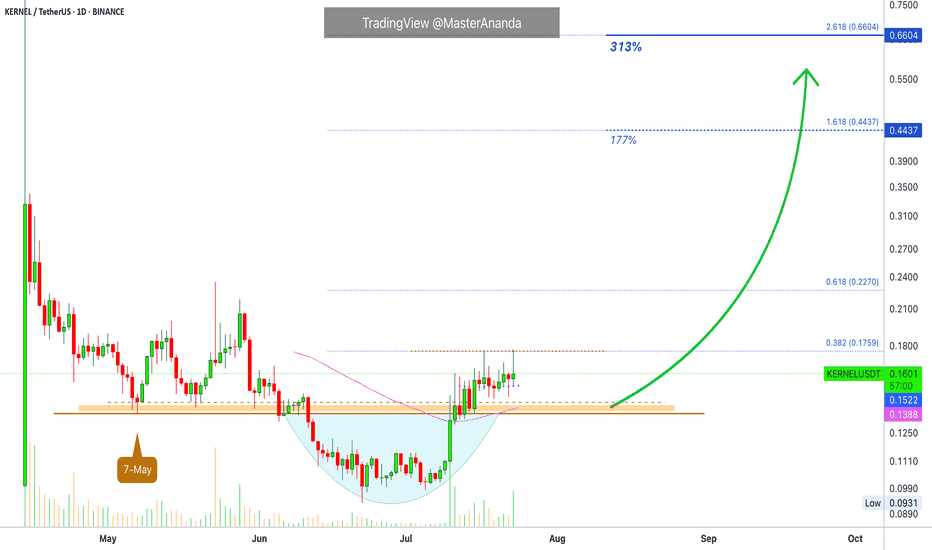
KernelDAO Short-Term Trade Setup · 300% Profits PotentialThis is another strong chart setup. I am looking at the short-term because that is the request I am getting from many of my followers. People are interested now in growing their capital so this can be used to accumulate strong reputable projects later on. Something like double-up, triple-up then grow some more. When enough cash is available; sit back, relax and hold.
The main low here is 7-May. The break below support is the liquidity-hunt event.
After the action recovers above support, bullish confirmed.
Notice KERNELUSDT trading above EMA55 and EMA89 daily.
Trading volume also favors the bullish side. Notice how red days have very low volume. On green days we have the higher numbers of volume spikes. High volume when buying, low volume when selling.
The first target is good and strong for 177%. The second target goes to 300%. This can be achieved easily within 1 month (short-term), or it can extend to two months but not much longer. The trick is to be ready to wait.
If you expect the market to move within hours or days, you might be disappointed. Yes, sometimes it moves fast but this is the exception and not the norm. Better to be prepared to wait a long time and if it moves faster, that's a bonus but we have to be realistic to produce consistent wins. If you want to be in the action, diversification is a good strategy. If you just want to win, patience is key.
Namaste.
WHY WILL IT GO HIGH?Reasons indicating strong potential:
- Large and active community on social media
- High scammer activity
- Trap for inexperienced users: selling on DEX at 3x lower price than on CEX due to low DEX liquidity
Let me know if you'd like it even more formal or formatted for a report.
So, what’s wrong with Kernel?Landscape in the agricultural sector could not be much more favourable for Kernel than it is nowadays. Grains Price Index is at its highest level since 2013 and the company has managed to fix most of its sale prices for the 2021/2022 season. According to the U.S. Department of Agriculture, global grain yields in 2021 will be remarkably high mostly thanks to the very impressive yields in Argentina and Ukraine. The other major producers like the United States, Brazil, Canada, and China faced unfavourable weather conditions in 2021. China is especially relevant in the context of Kernel as its agricultural products import increased in the first two quarters of 2021 by 34% y/y. Moreover, the key agricultural region of China, Henan province, experienced severe floods that are likely to facilitate the upward trend in the grains import. Let’s be more specific. Rather conservative DCF and comparables suggest a valuation of around 78PLN per share. Quite optimistic given the current 57.
So, what’s wrong with Kernel? The positive indicators I described have been widely known for quite some time however the share price does not display an upward trend. The late July price jump was caused by the buyback announcement. What is the market afraid of? One thing that comes to my mind is July’s Ukrainian tax authorities tax compliance check. Given the position of Kernel’s owner Andriy Verevskyi, I don’t believe that the firm can get busted on taxes. (Kernel is a huge VAT recipient*; more about Ukrainian oligarchs' power**). Donbas war could be considered another “risk factor” however, based on the media reports, the conflict smoulders rather than burns. Lastly, at the beginning of July Kernel announced the amendment of the expense plan regarding the new oilseed processing plant. Additional costs usually do not make shareholders particularly content although given the record yields this year, plant expansion seems to be justified.
Summing up, my valuation suggests that the business is undervalued and I can’t think of risks strong enough to justify current capitalization. Thus, I am optimistic.
*latifundist.com/en/novosti/56563-nazvany-krupnejshie-poluchateli-vozmeshcheniya-nds-v-agrosektore-za-avgust-2021-g
**chathamhouse.org/2021/07/ukraines-system-crony-capitalism/05-agriculture-counterexample
Generalized Moving Average Kernels
A moving averages is a very simple concept that traders often take for granted and do not consider the inner mechanics of. In a very generalized sense a moving average for the last n periods is something that combines the past n values with unique weightings for each value. The real power of a moving average is in how those weightings are chosen. In a larger sense our choice of weightings is called a "kernel" or an "envelope". So if we consider a simple moving average all the weightings are the same, which means that our calculation equally considers past price action and current price action, this has a flat kernel. A weighted or linear moving average (wma) has a kernel that is shaped like a line and is decreasing as the distance from the current bar increases that takes the form of y = mx+b. This means that the weighting is higher for more recent bars and less for historic bars; increasing the slope (the value "m") of this will make this kernel more sensitive to recent bars than past bars. The exponential moving average (ema) is theoretically just like the wma but with an exponential term, aka y = ax^2 + mx + b. increasing the value of "a" will make the average exponentially more sensitive to recent price action than past bars. These are just 3 examples of the most common kernels. However the choice in kernels can be entirely your choice, and this is what I am presenting to the tradingview community. These methods are rather common in the field of signal processing and hopefully trading sometime soon.
Here I have built 3 new kernels for everyone in an indicator I will release soon.
1. The generalized polynomial kernel (blue)
Whereas the wma is defined by y = mx + b, the ema by y = ax^2 + mx + b, the generalized polynomial kernel can take in an eighth order polynomial as a kennel function: y = sum (rx ^ i) where i ranges from 0 to 8 and the user has 9 coefficients "r". To make a wma here one just sets the last 6 values of r to zero, or to make an ema the user sets the last 5 values of r to zero. If you are curious what shape your polynomial makes you can just plug it into wolfram or google to see it. This is the blue line on the chart above with all coefficients set to 1 by default.
2. The gaussian kernel (red)
This option sets the moving average kernel to a gaussian. The important thing here to consider is where it is centered, and how broad it is. If the width of the gaussian is sufficiently larger than the moving average window size then you will start to approximate a simple moving average, however if the width of the gaussian is incredibly narrow you are basically sampling the bars from however long ago that your gaussian is centered, like creating an offset. If the centering is done closer to the recent bars then there is essentially a smooth drop off in weightings with a negative concavity. This is the red line on the chart.
3. The noise kernel (green)
The idea of this one is simple, to just make a random kernel. Any value of the kernel can have a vastly different weight than the neighboring kernels. As tradingview has no random number generator I used a quasi random one that multiplies the unix time with the price and takes the sine function of that. For being totally random it also appears to be useful. This is the green line on the chart.
The script for this will be coming soon, I just have to clean it up for everyone. Keep in mind that this indicator is not ready to just apply to the charts, it is designed for people to customize and mess with first.
If anyone has any ideas to test with this I am incredibly interested to explore this deeper. I am using this general idea to move onto very interesting and potentially powerful applications, if anyone wants to talk about the technicalities of these please feel free to message me.